| Discussion (0)How to Make Glossy Lipstick |
| Introduction |
Lipstick, or really just make up in general, is very difficult to create. The one look that's the most difficult as far as lipstick is concerned is a sheer glossy effect. In TS2 to create a lipgloss, you simply painted on a glossy lip texture and slapped it on the sim. However, in TS3 this is not the case. Really, no matter what you do to the lip overlay texture, it'll get washed out from the way TS3 renders its graphics. So instead of relying on the texture, you can manipulate the color channels via an RGB mask to "fake" a glossy shine. Like many other things when it comes to TS3 creation, I know the general "how-to" on creating glossy textures, however my own personal textures are far from perfect. This tutorial is simply to show the basics. Something that makes you go, "ahhhh, that's how it's done!" Then, it's up to you to take my basic instruction and apply it to something outstanding! :) |
| Credits/Acknowledgments |
Although all of my work is hand done by me, I would still like to credit Lemonleaf's Sims Cafe. I spent weeks studying how he/she did their lip textures, and after many attempts I feel confident enough to show what I've learned. |
| What You'll Need |
-- Adobe Photoshop (purchase) or GIMP 2.0 (free) --DDS Plug-in for Photoshop or GIMP (I'll be using Photoshop 7.0, so if you're using a different program the screen shots will be different but the concept is the same.) |
| Step 1: Prep-Work |
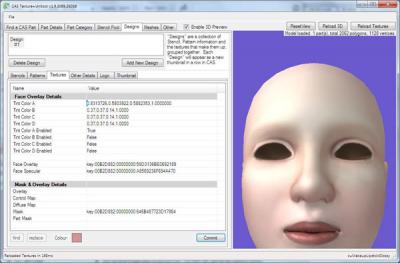
You'll need to extract a blank lip texture using the CAS creation program of your choice. I personally use the CAS Texture + Unitool (CTU), but you can use TSR Workshop or even S3PE if you choose, too. After you've extracted your lip texture, open it in your imaging program. |
| Step 1.1 |
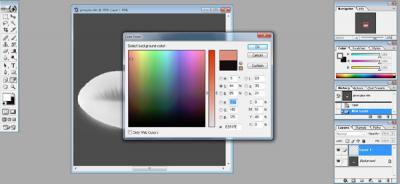
The key to getting a natural look to your lipgloss, or any makeup to be honest, is to use skintone colors on the base texture. So for starters I'm going to select a light pinkish/tanish color to use as the base color for the lip texture. If you're using Photoshop or a program that allows you to save color swatches, I would save your base color for later reference. <br clear="all"> |
| Step 2: Defining the Lips |
| Step 2.1 |
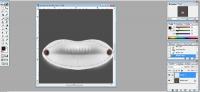
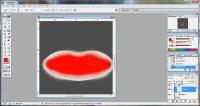
Make a new layer! In fact, for each step/addition create a new working layer. This is very important. ;) Adjust your base color to a dark hue that's not black. Draw in two large dots where the corners of the mouth are. Hint - To easily line up the mouth corners in photoshop, switch to the channels tab and ctrl + click the alpha channel layer. This should draw a fuzzy marquee around the lip area mapped out by the alpha channel. |
| Step 2.2 |
| Step 2.3 |
Merge the mouth corner layer and lip line layers together and go to Filters -> Gaussian Blur. Blur the line until a soft dark shadow is cast in between the lips. Note: The Gaussian blur filter may be located in a different menu if using a program other than Photoshop. |
| Step 2.4 |
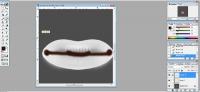
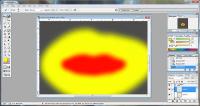
Using the same dark color as before redraw the mouth corners, this time a little smaller. Then, draw a slightly thinner line, like before, in between the lips. Defining the top and bottom lips, in my opinion, is what gives the lipgloss a more natural appearance. Without the "lip lining" your sims' lips will look like one big mass of color, instead of as two separate forms. |
| Step 3: Pucker Up! |
| Step 3.1 |
| Step 3.2 |
| Step 3.3 |
| Step 3.4 |
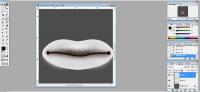
Once you've given your lips some texture, you need to go back and add the highlights. Remember that one of the more important highlights on the lips in the on on the top center of the upper lip. To create it you essentially draw a small white moon on the top of the lip texture. Use the Ctrl + Click method to get it lined up right. With a bit of fiddling around, this is what I've came up with as far as highlights and shine. |
| Step 3.5 |
| Step 4: Make Some Noise! |
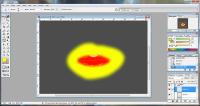
This next step is essential to preserve the lipgloss texture when in game! Go to the filters menu and look for the Noise filter. Adding a little noise to the texture keeps the game from blurring the texture and making it one big mess. Either apply the filter to each layer, or if you're feeling confident you can merge all layers and apply the filter to it as a whole. Just add a small amount of noise! A good way to judge what's a fair amount is to learn as far back in your chair as you can and slightly squint your eyes. If you can still make out the texture, then you're okay. |
| Step 5: Creating the RGB Mask |
| Please Note |
As i stated in the introduction, the RGB mask is what actually give the lipgloss it's "shine". You have to manipulate the channels to give you the desired look. In my tutorial, I'm showing you how I made my mask for this particular lipstick. Depending on your personal style and design, your mask may differ. |
| Step 5.1 |
| Step 5.2 |
| Step 5.3 |
| Step 5.4 |
Save your mask as a DXT1|No Alpha an import it into your CAS creation program. |
| Step 5.5 |
| Finishing Up |
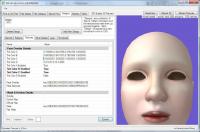
My tutorial is just a quick and dirty one, which means that in order to get yours looking fabulous, you'll have to play around with it for a bit and tweak pieces here and there. After fixing a few small issues, I packaged my lipgloss, and here's what it looks like in game: Thanks for reading! Now go gloss some lips! |
| Special gift for you! |
If for some reason you want this lipgloss, you can download it exclusively from LeeFish |
| Categories |
| Editor Bar |



 Versions
Versions Last changes
Last changes All articles
All articles Categories
Categories